Mathematical problems can and do arise naturally within art and design contexts. For example, last week's reading likely left you with numerical questions like: Why does a satin weave call for a minimum of 5 warp and weft threads? Why does it demand "two groups of different size that are larger than one thread, that are not divisible one into the other, and that are not divisible by a common third"? What is the math content of the last sentence? Etc.

We can and will take up these questions eventually, but first I want to take a step back from the application of math to precise questions in art and design. I want to consider a more basic question about math and creativity, namely: how do you make something new with old tools? For this we will turn to a student of Pólya by the name of Imre Lakatos.

Lakatos' book Proofs and Refutations is a historical reenactment of the evolution of the Euler-Descartes theorem, a deep and far-reaching fact about the geometry of solids. The book not only validates Pólya's characterization of problem-solving via heuristics, it also illuminates how mathematics finds the problems it pursues. It presents a dynamic process of math in the making.

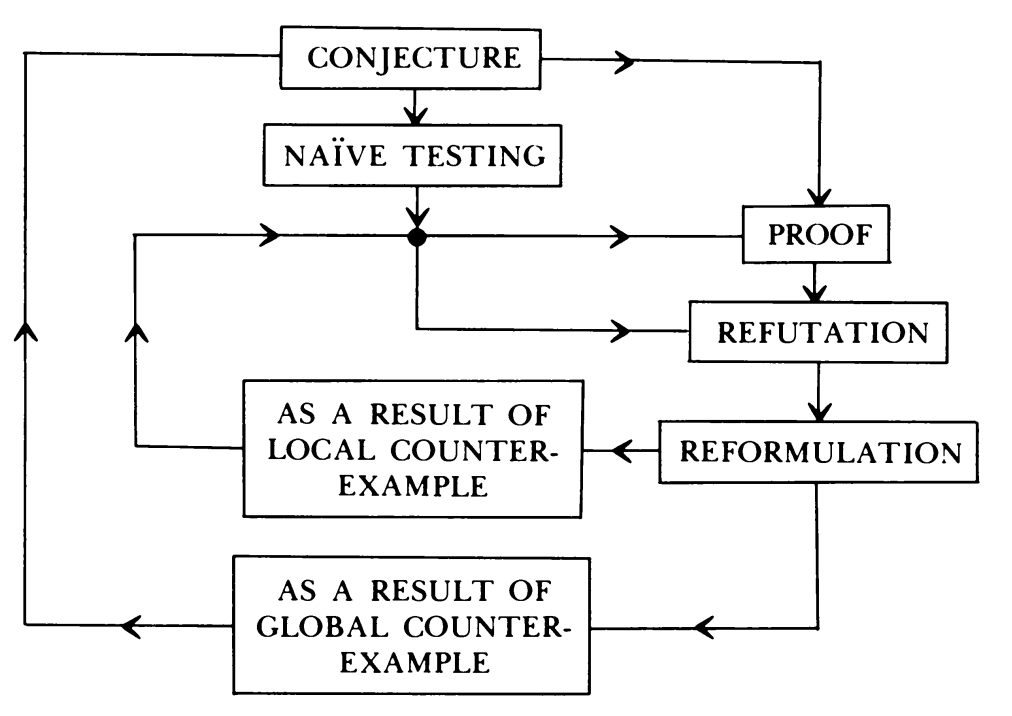
In case you wondered whether math's only use was to address static and narrow questions, or worse, to certify truths already believed, you may find Lakatos surprising. You may even begin to find it harder to distinguish math from art and design.