This class will pursue open-ended mathematical problems inspired by the interdisciplinary experiments of scientists, designers, artists, and students at Black Mountain College (1933-1957).
Problems like the “meander” question posed by BMC mathematician, Max Dehn:
...how to draw a stripe of unit width in a square lattice between two parallel lines separated by n units so that the stripe (the Meander River) fills the band...
To illustrate the question, Dehn drew this example: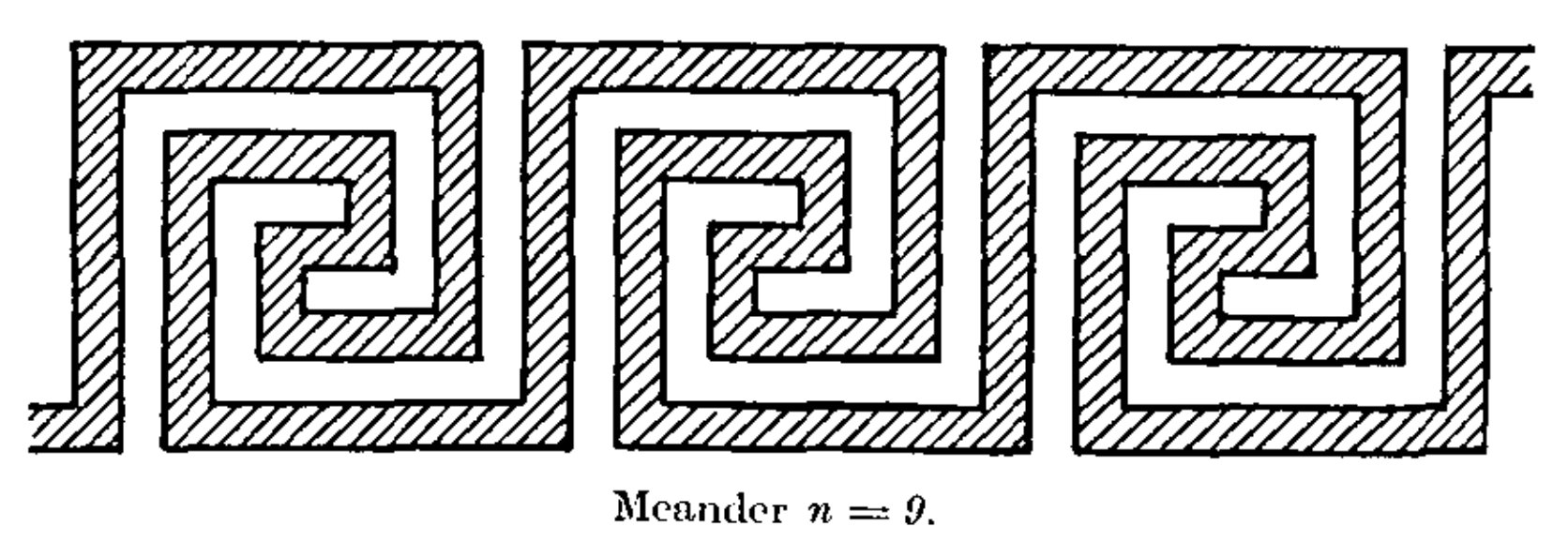
Often our first move when presented with a problem in this class will be to draw further examples. Drawing meanders by hand was typical of the “handicraft instruction” of Josef Albers, the artist and educator responsible for organizing the arts curriculum at the center of Black Mountain College.
This page of student notes by Lore Kadden Lindenfeld from Albers's 1945 Basic Design class shows how a form can evolve through a variant series.
Variations, in turn, often prompt further questions, like: What if n is not equal to 9? What if the lattice is not square? What if my meander decides to reverse the direction of its spiral? How is it that "one line produces the effect of two"?
Both Dehn and Albers found in the meander an elementary expression of a type of problem that concerns the relationship between things, a situational problem, a problem of configuration.
August 27, 2025
Overview
Overview
Reading
The Topology of Roman Mosaic Mazes (Anthony Phillips)
Resources
A Key (Robert Wiesenberger)